原理介绍

基础原理这里不再概述

介绍对于点在多边形顶点，点在边上等判断方法

  1. 判断点是否在线上的方法有很多，比较简单直接的就是计算点与两个多边形顶点的连线斜率是否相等，中学数学都学过
  2. 点和多边形顶点重合的情况更简单，直接比较点的坐标就行了
  3. 顶点穿越看似棘手，其实我们换一个角度，思路会大不相同。先来回答一个问题，射线穿越一条线段需要什么前提条件？没错，就是线段两个端点分别在射线两侧。只要想通这一点，顶点穿越就迎刃而解了。这样一来，我们只需要规定被射线穿越的点都算作其中一侧。

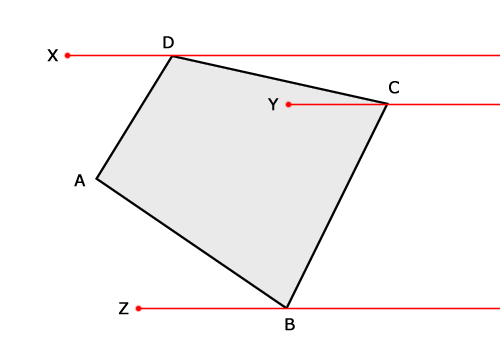
如上图，假如我们规定射线经过的点都属于射线以上的一侧，显然点D和发生顶点穿越的点C都位于射线Y的同一侧，所以射线Y其实并没有穿越CD这条边。而点C和点B则分别位于射线Y的两侧，所以射线Y和BC发生了穿越，由此我们可以断定点Y在多边形内。同理，射线X分别与AD和CD都发生了穿越，因此点X在多边形外，而射线Z没有和多边形发生穿越，点Z位于多边形外。

  1. 解决了第三点，这一点就毫无难度了。根据上面的假设，射线连续经过的两个顶点显然都位于射线以上的一侧，因此这种情况看作没有发生穿越就可以了。由于第三点的解决方案实际上已经覆盖到这种特例，因此不需要再做特别的处理。

代码实现

C++再MFC中的实现:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
string PointJudge(POINT p, POINT* poly, int ploySize) {
    /*
    * @param {POINT} p  待判断点的坐标。
    * @param {POINT *} poly  多边形各点的坐标集合
    * @param {int} polySize 多边形边的数量（多边形顶点的数量）
    */
    int px = p.x;
    int py = p.y;
    bool flag = false;
    int i, l, j;
    for (i = 0,  l = ploySize,  j = l - 1; i < l; j = i, i++) {
        int sx = poly[i].x;
        int sy = poly[i].y;
        int tx = poly[j].x;
        int ty = poly[j].y;
        if ((sx == px && sy == py) || (tx == px && ty == py)) {
            return "内部";
        }
        if ((sy < py && ty >= py) || (sy >= py && ty < py)) {
            int x = sx + (py - sy) * (tx - sx) / (ty - sy);
            if (x == px) {
                return "边上";
            }
            if (x > px) {
                flag = !flag;
            }
        }
    }
    return flag%2 != 0 ? "内部" : "外部";
}

JavaScript实现:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
/**
 * @description 射线法判断点是否在多边形内部
 * @param {Object} p 待判断的点，格式：{ x: X坐标, y: Y坐标 }
 * @param {Array} poly 多边形顶点，数组成员的格式同 p
 * @return {String} 点 p 和多边形 poly 的几何关系
 */
function rayCasting(p, poly) {
  var px = p.x,
      py = p.y,
      flag = false

  for(var i = 0, l = poly.length, j = l - 1; i < l; j = i, i++) {
    var sx = poly[i].x,
        sy = poly[i].y,
        tx = poly[j].x,
        ty = poly[j].y

    // 点与多边形顶点重合
    if((sx === px && sy === py) || (tx === px && ty === py)) {
      return 'on'
    }

    // 判断线段两端点是否在射线两侧
    if((sy < py && ty >= py) || (sy >= py && ty < py)) {
      // 线段上与射线 Y 坐标相同的点的 X 坐标
      var x = sx + (py - sy) * (tx - sx) / (ty - sy)

      // 点在多边形的边上
      if(x === px) {
        return 'on'
      }

      // 射线穿过多边形的边界
      if(x > px) {
        flag = !flag
      }
    }
  }

  // 射线穿过多边形边界的次数为奇数时点在多边形内
  return flag ? 'in' : 'out'
}