什么是KMP
说到JKMP,先说一下KMP这个名字是怎么来的, 为什么叫做KMP呢。
因为这是由三位学者发明的:Knuth, Morris和Pratt,所以娶了三位学者名字的首字母,叫做KMP。
KMP主要有什么应用
KMP主要应用在字符串匹配上。
KMP的主要思想是当出现字符串不匹配时,可以知道一部分之前已经匹配的文本内容,可以利用这些信息避免从头再去做匹配。
所以如何记录已经匹配的文本内容,是KMP算法的重点,也是next数组肩负的重任。
什么是前缀表
写过KMP的同学,一定都写过next数组,那么这个next数组究竟是个什么东西?
next数组就是一个前缀表(prefix table)。
前缀表有什么用呢?
前缀表是用来回溯的,它记录了模式串与主串(文本串)不匹配的时候,模式串应该从哪里开始重新匹配。
为了清楚的了解前缀表的来历,我们来举一个例子:
要在文本串:aabaabaaf中查找是否出现过一个模式串:aabaf。
请记住文本串和模式串的作用:
要在文本串:aabaabaaf中查找是否出现过一个模式串:aabaaf。
如动画所示:

动画里,我特意把 子串aa 标记上了,这是有原因的,大家先注意一下,后面还会说道。
可以看出,文本串中第六个字符b 和 模式串的第六个字符f,不匹配了。如果暴力匹配,会发现不匹配,此时就要从头匹配了。
但如果使用前缀表,就不会从头匹配,而是从上次已经匹配的内容开始匹配,找到了模式串中第三个字符b继续开始匹配。
此时就要问了「前缀表是如何记录的呢?」
首先要知道前缀表的任务是当前位置匹配失败,找到之前已经匹配上的位置,在重新匹配,此也意味着在某个字符失配时,前缀表会告诉你下一步匹配中,模式串应该跳到哪个位置。
那么什么是前缀表:「下表i之前(包括i)的字符串中,有多大长度的相同前缀后缀。」
为什么一定要用前缀表
这就是前缀表那为啥就能告诉我们 上次匹配的位置,并跳过去呢?
回顾一下,刚刚匹配的过程在下表5的地方遇到不匹配,模式串是指向f,如图:
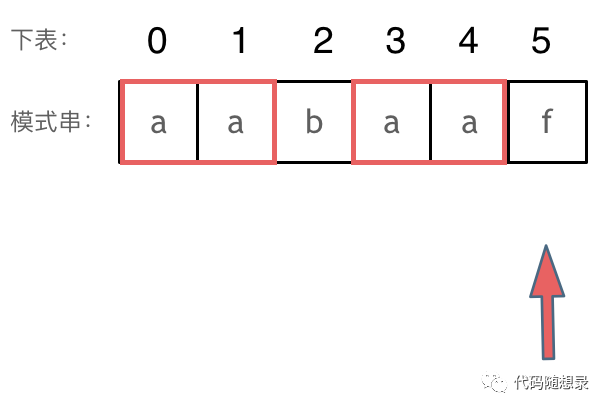
然后就找到了下表2,指向b,继续匹配:如图:
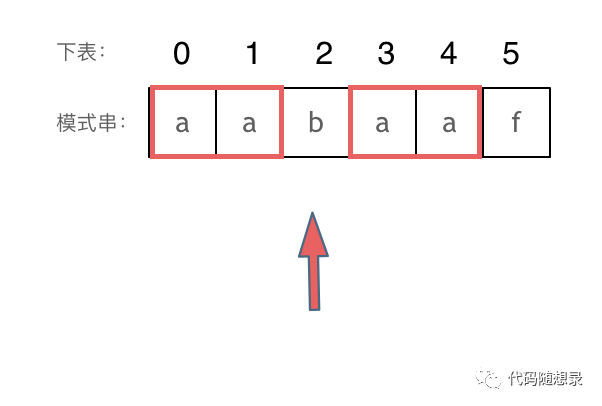
以下这句话,对于理解为什么使用前缀表可以告诉我们匹配失败之后跳到哪里重新匹配 非常重要!
「下表5之前这部分的字符串(也就是字符串aabaa)的最长相等的前缀 和 后缀字符串是 子字符串aa ,因为找到了最长相等的前缀和后缀,匹配失败的位置是后缀子串的后面,那么我们找到与其相同的前缀的后面从新匹配就可以了。」
所以前缀表具有告诉我们当前位置匹配失败,跳到之前已经匹配过的地方的能力。
「很多介绍KMP的文章或者视频并没有把为什么要用前缀表?这个问题说清楚,而是直接默认使用前缀表。」
如何计算前缀表
接下来就要说一说怎么计算前缀表。
如图:
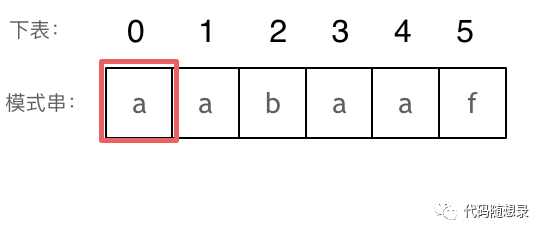
长度为前1个字符的子串a,最长相同前后缀的长度为0。(注意这里计算相同前后缀,不算重复的字符)
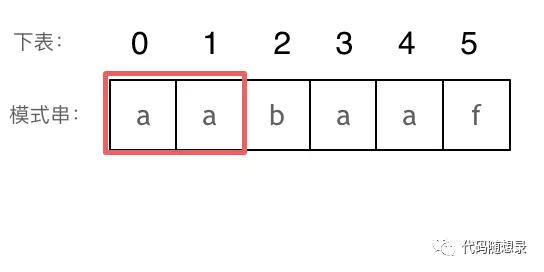
长度为前2个字符的子串aa,最长相同前后缀的长度为1。
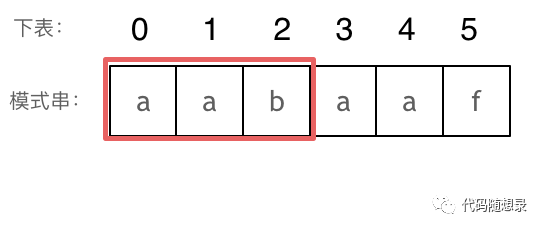
长度为前3个字符的子串aab,最长相同前后缀的长度为0。
以此类推:
长度为前4个字符的子串aaba,最长相同前后缀的长度为1。
长度为前5个字符的子串aabaa,最长相同前后缀的长度为2。
长度为前6个字符的子串aabaaf,最长相同前后缀的长度为0。
那么把求得的最长相同前后缀的长度就是对应前缀表的元素,如图:
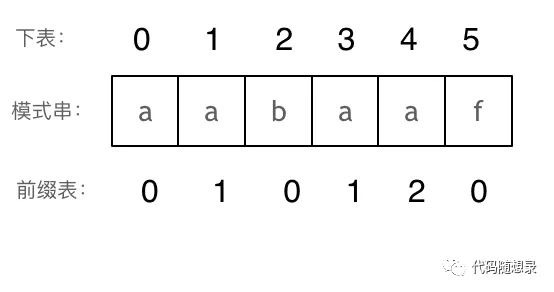
可以看出「前缀表里的数值代表着就是:当前位置之前的子串有多大长度相同的前缀后缀。」
再来看一下如何利用 前缀表找到 当字符不匹配的时候应该指针应该移动的位置。如动画所示:
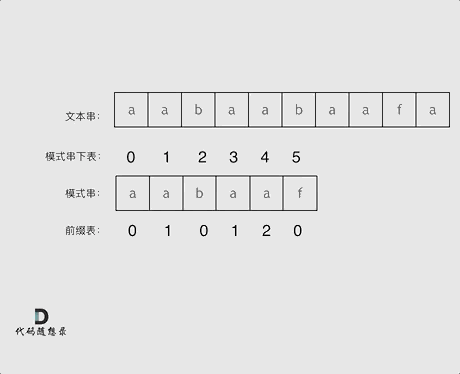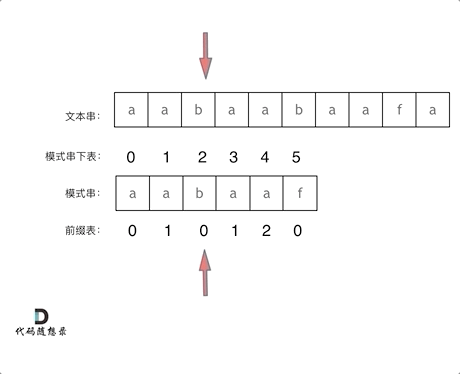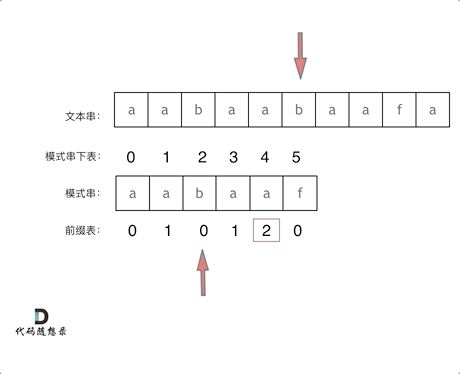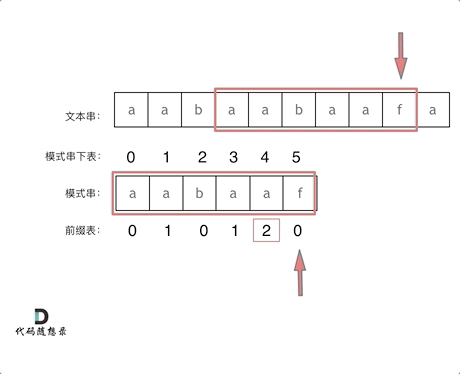
找到的不匹配的位置, 那么此时我们要看它的前一个字符的前缀表的数值是多少。
为什么要看前一个字符的前缀表的数值呢,因为要找前面字符串的最长相同的前缀和后缀。
所以要看前一位的 前缀表的数值。
前一个字符的前缀表的数值是2, 所有把下表移动到下表2的位置继续比配。可以再反复看一下上面的动画。
最后就在文本串中找到了和模式串匹配的子串了。
前缀表有什么问题
来看一下刚刚求的这个前缀表有什么问题呢?
如图:
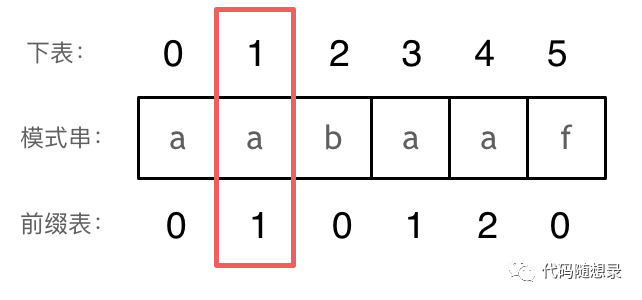
看这个位置红框的位置,如果要找下表1 所对应 前缀表里的数值的时候,前缀表里的数值依然是1,然后就要跳到下表1的位置,如此就「形成了一个死循环」。
「如何怎么避免呢,就把前缀表里的数值统一减一, 开始位置设置为-1 。」 这一点对理解后面KMP代码很重要!!
改为如图所示:
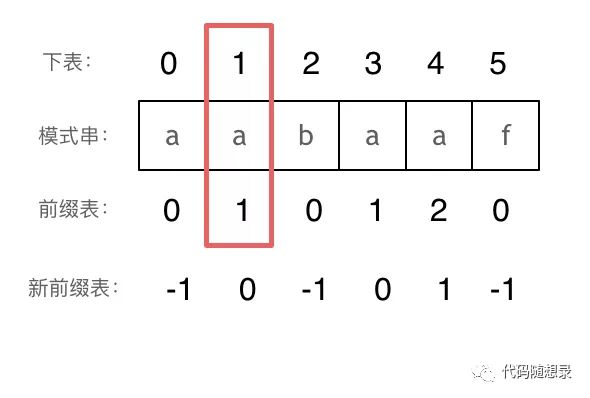
这样就避免的死循环,只不过后续取 前缀表里的数值的时候,要记得再+1,才是我们想要的值。
「最后得到的新前缀表在KMP算法里通常用一个next数组来表示。」
注意这个next数组就根据模式串求取的。
使用next数组来匹配
有了next数组,就可以根据next数组来 匹配文本串s,和模式串t了。
注意next数组是新前缀表(旧前缀表统一减一了)。
匹配过程动画如下:
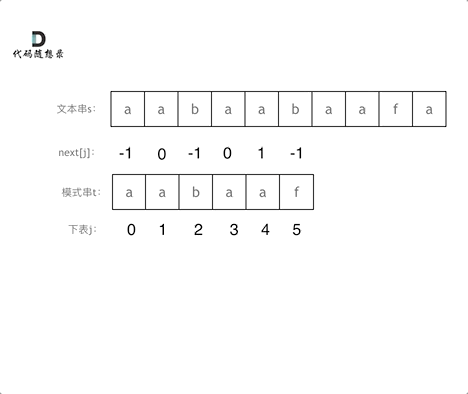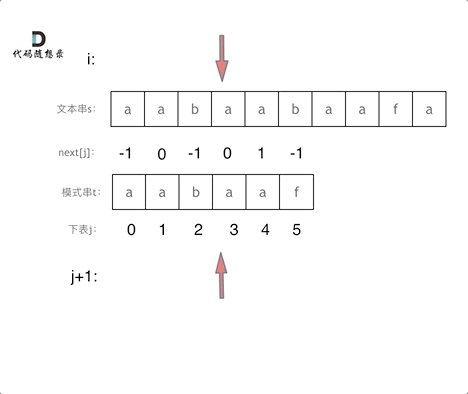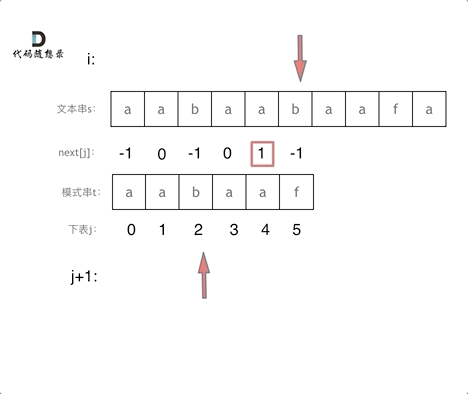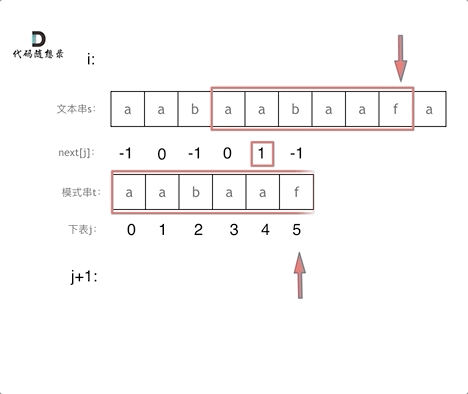
时间复杂度分析
再来看一下时间复杂度, 假设文本串长度为n,模式串长度为m,动画为上图。
其中n为文本串长度,m为模式串长度,因为在匹配的过程中,根据前缀表不断调整匹配的位置,可以看出匹配的过程是O(n),但之前还要单独生成next数组,时间复杂度是O(m)(next数组的实现代码将在后续文章中继续讲解),所以整个KMP算法的时间复杂度是O(n+m)的。
暴力的解法显而易见是O(n * m),所以「KMP在字符串匹配中极大的提高的搜索的效率。」
文章转自代码随想录,原文链接