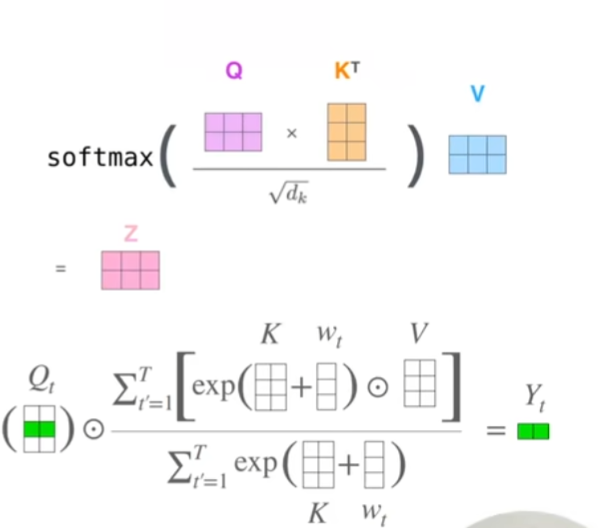
图中上部分是标准的Attention，下部分是AFT Attention

Transformer Attention向量版：

$$\mathrm{Attn}(Q,K,V)t=\frac{\sum{i=1}^Te^{q_t^\top k_i}v_i}{\sum_{i=1}^Te^{q_t^\top k_i}}.$$

1
2
3
4
5
6
7
8
9
10
11
12
# equation 8: self-attention as vector operations
O = torch.zeros(T, D)
for t in range(T):
    Z = 0
    ot = torch.zeros(D)
    for i in range(T):
        att = (Q[t] @ K[i]).exp()
        ot += att * V[i]
        Z += att
    ot /= Z
    O[t] = ot
print(O)

代码中，O是注意力矩阵，对每个token，初始化注意力向量，然后从第一个token往后遍历，计算当前token与第i个token的注意力分数，最后乘以V[i]，再进行归一化处理。

1
2
3
4
5
# standart self-attention 矩阵版
attn = torch.softmax(Q @ K.t(), dim=-1)
O_sa = attn @ V
print(O_sa)
assert torch.allclose(O, O_sa)

AFT的线性Attention：

$$\mathrm{Attn}^+(W,K,V)t=\frac{\sum{i=1}^te^{w_{t,i}+k_i}v_i}{\sum_{i=1}^te^{w_{t,i}+k_i}}$$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
# attention free transformer
O_aft = torch.zeros(T, D)
# pair-wise position bias

W = torch.randn(T, T) ## 这里相当于是创建了一个token和token之间的偏置矩阵，模型就是要学习这个固定的静态的偏置
for t in range(T):
    Z_aft = 0
    o_aft = torch.zeros(D)
    for i in range(t+1):
        att_aft = (W[t, i] + K[i]).exp()
        o_aft += att_aft * V[i]
        Z_aft += att_aft
    O_aft[t] = o_aft / Z_aft
print(O_aft)

线性attention，就是取消了Q，将其替换为了w，即token与token之间的偏置值，是模型要学习的部分。

RWKV的线性Attention：

$$wkv_t=\frac{\sum_{i=1}^{t-1}e^{-(t-1-i)w+k_i}v_i+e^{u+k_i}\odot v_t}{\sum_{i=1}^{t-1}e^{-(t-1-i)w+k_i}+e^{u+k_i}}$$

1
2
3
# set W and U first
W_rwkv = torch.randn(D)
U_rwkv = torch.randn(D)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
# rwkv attention
# 随时间u, 0, -w, -2w这样衰减
# exp(u+k)v + exp(k)v + exp(-w+k)v + exp(-2w+k)v
O_rwkv = torch.zeros(T, D)
for t in range(T):
    Z_rwkv = 0
    O_rwkv_t = torch.zeros(D)
    for i in range(t):
        att_rwkv = (-(t-(i+1)) * W_rwkv + K[i]).exp()
        O_rwkv += att_rwkv * V[i]
        Z_rwkv += att_rwkv
    att_rwkv = (U_rwkv + K[t]).exp()
    O_rwkv += att_rwkv * V[t]
    Z_rwkv += att_rwkv
    O_rwkv[t] = O_rwkv_t / Z_rwkv
print(O_rwkv)

##
o0 = (U_rwkv + K[0]).exp() * V[0]
## so a0 = 0
#
o1 = (K[0]).exp() * V[0] + (U_rwkv + K[1]).exp() * V[1]
a1 = (K[0]).exp() * V[0]
# print(1, a1)
o2 = (-W_rwkv + K[0]).exp() * V[0] + (K[1]).exp() * V[1] + (U_rwkv + K[2]).exp() * V[2]
a2 = (-W_rwkv + K[0]).exp() * V[0] + (K[1]).exp() * V[1]
# print(2, a2)

RWKV这里的也是没有Q，但是多了W和U，其中W是时间衰减向量，他的意思就是，比如我给的当前token一个bonus(奖励)即U，那么认为当前token是对模型更重要的，之前的token的注意力分数按照当前是U，上一个是0， 上上一个是-W，再往前一个是-2W这样进行时间衰减。

RWKV可以写成RNN的递归形式

$$wkv_t=\frac{a_{t-1}+e^{u+k_t}\odot v_t}{b_{t-1}+e^{u+k_t}}$$
$$a_t=e^{-w}\odot a_{t-1}+e^{k_t}\odot v_t$$
$$b_t=e^{-w}\odot b_{t-1}+e^{k_t}$$

1
2
3
4
5
6
7
8
9
10
11
# rwkv attention
O_rwkv = torch.zeros(T, D)
O_rwkv[0] = V[0]
# a0, b0 not zero, but
a = (K[0]).exp() * V[0]
b = (K[0]).exp()
for t in range(1, T):
    O_rwkv[t] = (a + torch.exp(U_rwkv + K[t]) * V[t]) / (b + torch.exp(U_rwkv + K[t]))
    a = torch.exp(-W_rwkv) * a + torch.exp(K[t]) * V[t]
    b = torch.exp(-W_rwkv) * b + torch.exp(K[t])
print(O_rwkv)

RNN的递归形式，相当于是将a和b当做RNN 中的state或者理解成cache也可以，来进行传递，能够减少计算量。

数值稳定版

exp(k)很容易溢出，特别是float16（最大数字是65504）训练时，所以我们还需要对代码进行一些改造

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
#RWKV attenton
O_rwkv = torch.zeros(T, D)
#init

pp = K[0]
aa = V[0]
bb = 1
O_rwkv[0] = V[0]
for t in range(1, T):
    ww = U_rwkv + K[t]
    qq = torch.max(ww, pp)
    e1 = torch.exp(pp - qq)
    e2 = torch.exp(ww - qq)
    a = e1 * aa + e2 * V[t]
    b = e1 * bb + e2
    O_rwkv[t] = a / b
    ww = pp - W_rwkv
    qq = torch.maximum(ww, K[t])
    e1 = torch.exp(ww - qq)
    e2 = torch.exp(K[t] - qq)
    aa = e1 * aa + e2 * V[t]
    bb = e1 * bb + e2
    pp = qq
print(O_rwkv)